
So, in \(ΔACE,\) we have \(AE=AC\) (Sides opposite to equal angles are equal)Īccording to the basic proportionality theorem, if a line is drawn parallel to one side of the triangle, then it divides the other two sides in the same ratio. A midpoint is the point that divides a line segment into two congruent line segments. Hence, \(ΔACE\) is an isosceles triangle. Midpoint of a segment, The point where a bisector intersects a segment Perpendicular Bisector, A bisector that is perpendicular to a segment Angle Bisector, A.
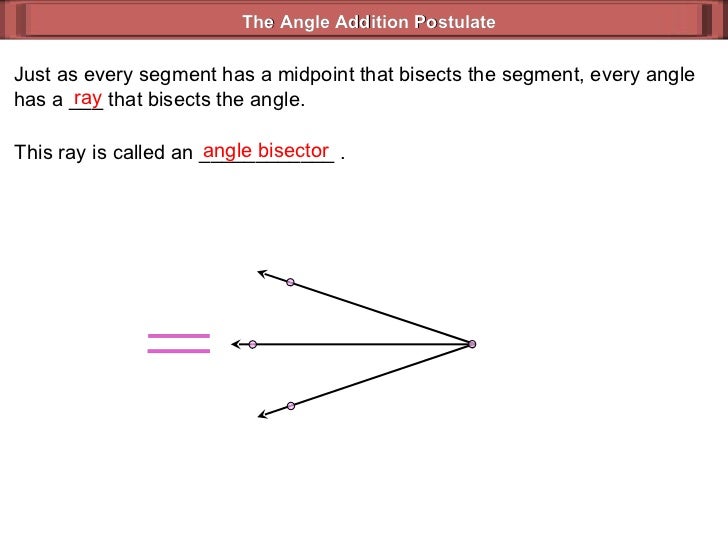
Given, \(AD\) is the angle bisector of \(∠CAP,\) For example, an angle bisector of a 60-degree angle will divide it into two angles of 30 degrees each.
#BISECTOR POSTULATE DEFINITION GEOMETRY HOW TO#
Learn how to create a perpendicular bisector, understand its definition, and and see some real-life examples. Similarly, \(CE\parallel DA\) and \(BP\) is transversal. What is Angle Bisector The angle bisector in geometry is the ray, line, or segment which divides a given angle into two equal parts. A perpendicular bisector is used in geometry theorems, proofs, and constructions. \(∠ECA=∠CAD\) (Alternate angles)\(……….(1)\) One of the most fundamental theorems in mathematics, particularly in geometry, is the Angle Bisector Theorem.
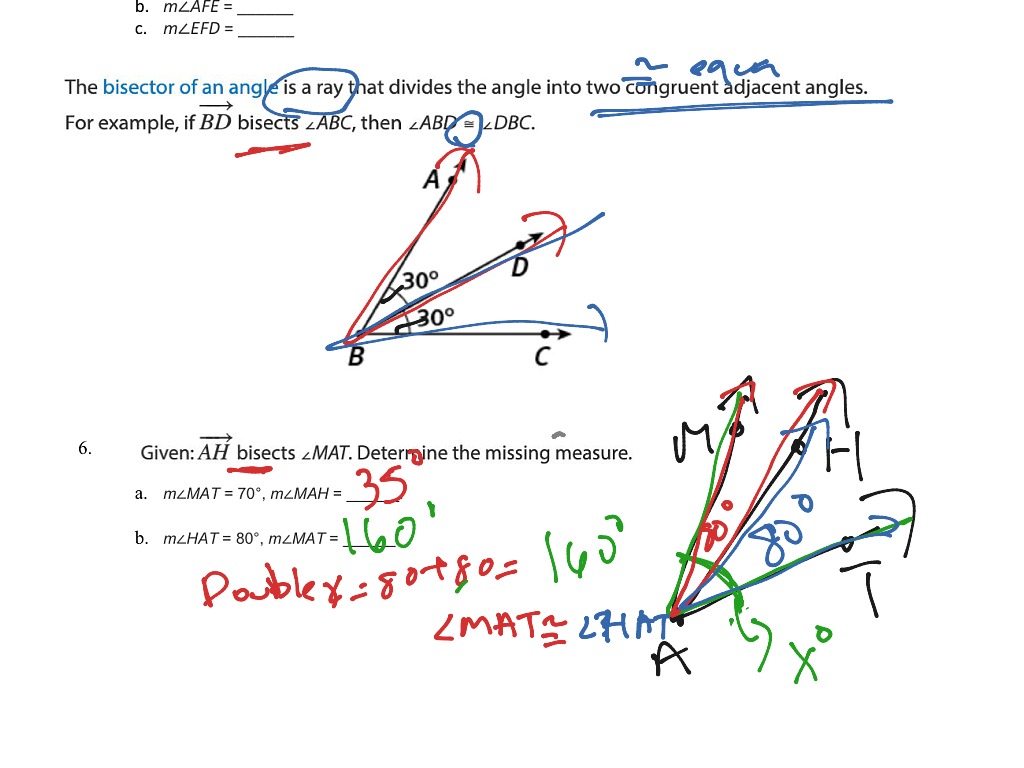
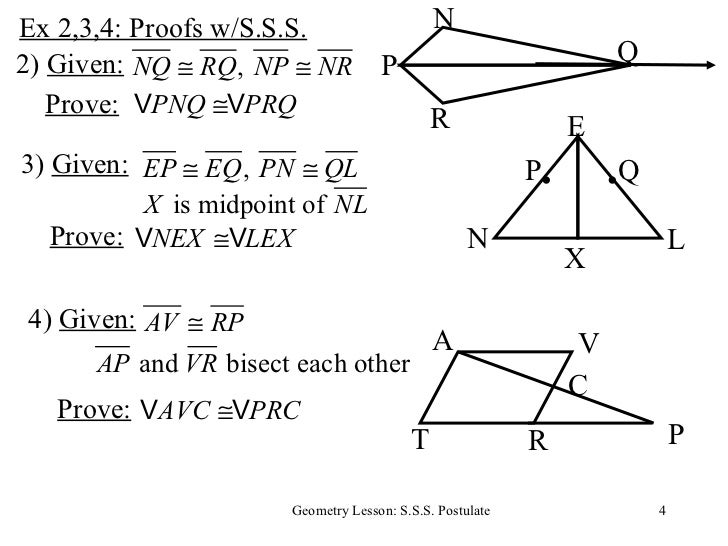
From the figure,\(CE\parallel DA\) and \(AC\) is transversal, and we know that alternate interior angles formed by a transversal are equal.


 0 kommentar(er)
0 kommentar(er)
